選択した画像 trig identity 1 tan^2x 169174-Trig identities 1+tan^2x

Pythagorean identities are identities in trigonometry that are extensions of the Pythagorean theorem The fundamental identity states that for any angle θ, \theta, θ, cos ⁡ 2 θ sin ⁡ 2 θ = 1 \cos^2\theta\sin^2\theta=1 cos2 θsin2 θ = 1 Pythagorean identities are useful in simplifying trigonometric expressions, especially inTrigonometric Identities Solver \square!Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!

Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x

Trig identities 1+tan^2x

Trig identities 1+tan^2x-Tan (2x) = 2 tan (x) / (1 tan ^2 (x)) sin ^2 (x) = 1/2 1/2 cos (2x) cos ^2 (x) = 1/2 1/2 cos (2x) sin x sin y = 2 sin ( (x y)/2 ) cos ( (x y)/2 ) cos x cos y = 2 sin ( (x y)/2 ) sin ( (x y)/2 ) Trig Table of Common Angles angleTrigonometric Simplification Calculator \square!

Understanding Pythagorean Identities Studypug

The inverse trigonometric identities or functions are additionally known as arcus functions or identities Fundamentally, they are the trig reciprocal identities of following trigonometric functions Sin Cos Tan These trig identities are utilized in circumstances when the area of the domain area should be limited These trigonometry functions have extraordinary noteworthiness 1tan^2x=sec^2x Change to sines and cosines then simplify 1tan^2x=1(sin^2x)/cos^2x =(cos^2xsin^2x)/cos^2x but cos^2xsin^2x=1 we have1tan^2x=1/cos^2x=sec^2x Trigonometry Science(b) 3cos2 x−sin2 x =1 − π 2

It can be concluded that, tan A = 3/4 Now, using the trigonometric identity 1tan2 a = sec2 a sec2 A = 1 (3/4)2 sec 2 A = 25/16 sec A = ±5/4 Since, the ratio of lengths is positive, we can neglect sec A = 5/4 Therefore, sec A = 5/4Question 12 SURVEY 60 seconds Q Simplify this to a basic trigonometry function tan (x)csc (x) answer choices tanx secx cotxO A Pythagorean Identity OB Quotient Identity OC

Basic trigonometric identities Common angles Degrees 0 30 45 60 90 Radians 0 ˇ 6 ˇ 4 ˇ 3 ˇ 2 sin 0 1 2 p 2 2 p 3 2 1 cos 1 p 3 2 p 2 2 1 2 0 tan 0 p 3 3 1 p 3 Reciprocal functions cotx= 1 tanx cscx= 1 sinx secx= 1 cosx Even/odd sin( x) = sinx cos( x) = cosx tan( x) = tanx Pythagorean identities sin2 xcos2 x= 1 1tan2 x= sec2 x 1cot2 xTrigonometry questions and answers Verify each identity sin 2x cos 2x1 =tan x b) tan xcotx tan xcotx 2 sinºx1Prove the trigonometric identity 1/ (sin (x)^2cos (x)^2)= (cot (x)^2)/ (1cot (x)^2) (tan (x)^2)/ (1tan (x)^2) SnapXam

Tangent Half Angle Formula Wikipedia

List Of Trigonometric Identities Wikipedia

The basic trigonometric functions include the following \(6\) functions sine \(\left(\sin x\right),\) cosine \(\left(\cos x\right),\) tangent \(\left(\tan x\rightThis is probably the most important trig identity Identities expressing trig functions in terms of their complements There's not much to these Each of the six trig functions is equal to its cofunction evaluated at the complementary angle Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2π while tangent and1 cos ( x) − cos ( x) 1 sin ( x) = tan ( x) Go!

O Trigonometric Identities And Equations Verifying A Trigonometric Identity Complete The Proof Of The Identity By Homeworklib

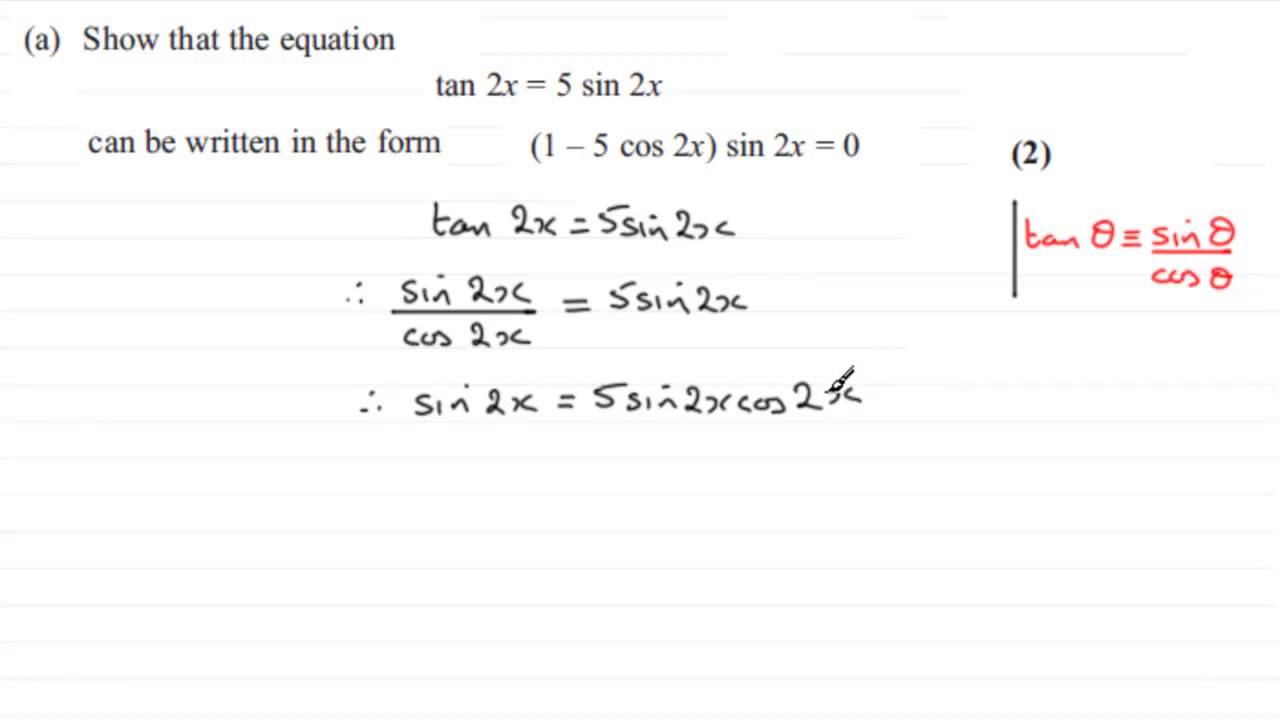
Exam Questions Trigonometric Identities Examsolutions

Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange1 a2 x2 dx We make the substitution x = atanθ, dx = asec2 θdθ The integral becomes Z 1 a2 a2 tan2 θ asec2 θdθ and using the identity 1tan2 θ = sec2 θ this reduces to 1 a Z 1dθ = 1 a θ c = 1 a tan−1 x a c This is a standard result which you should be aware of and be prepared to look up when necessary Key Point Z 1 1x2 dx = tan−1 x c Z 1 a2 x2 dx = 1 a tan−1 x a cProving Trigonometric Identities Calculator Get detailed solutions to your math problems with our Proving Trigonometric Identities stepbystep calculator Practice your math skills and learn step by step with our math solver Check out all of our online calculators here!

Understanding Pythagorean Identities Studypug

3 Simplifying Trig Expression 1 Tan 2x Youtube

 This question is easily solve by factoring and knowing that $1\tan^2{x}=\sec^2x$ $$\frac{\sin x\sin x \tan^2x}{\tan x}=\frac{\sin x (1\tan^2x)}{\tan x}$$ $$\frac{\sin x \sec^2x}{\tan x}=\frac{\tan x \sec x}{\tan x}=\sec x=\boxed{\frac{1}{\cos x}}$$ In almost any mathematics excersise you should factorize whenever you can, it gives you a wider view of the2sin2 x cosx = 1 for values of x in the interval 0 ≤ x < 2π Using the identity sin2 x cos2 x = 1 we can rewrite the equation in terms of cosx Instead of sin2 x we can write 1− cos2 x Then 2sin2 x cosx = 1 2(1− cos2 x)cosx = 1 2−2cos2 x cosx = 1 This can be rearranged to 0 = 2cos2 x −cosx− 1 You can check some important questions on trigonometry and trigonometry all formula from below 1 Find cos X and tan X if sin X = 2/3 2 In a given triangle LMN, with a right angle at M, LN MN = 30 cm and LM = 8 cm Calculate the values of sin L, cos L, and tan L 3

Answered O Trigonometric Identities And Bartleby

Trigonometric Identities Edexcel A Level Maths Pure Revision Notes

 $$\frac{ \cos 2x}{1\sin 2x}=\tan\left(\frac{\pi}{4}x\right)$$ Hi I'm confused how to prove this trig identity for the left side If someone could Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin ⁡ \sin sin andAnswer to Verify the identity \\frac{1}{1 \\sin^2x} = 1 \\tan^2x By signing up, you'll get thousands of stepbystep solutions to your homework

7 Proving Ids Trig Functions Identities

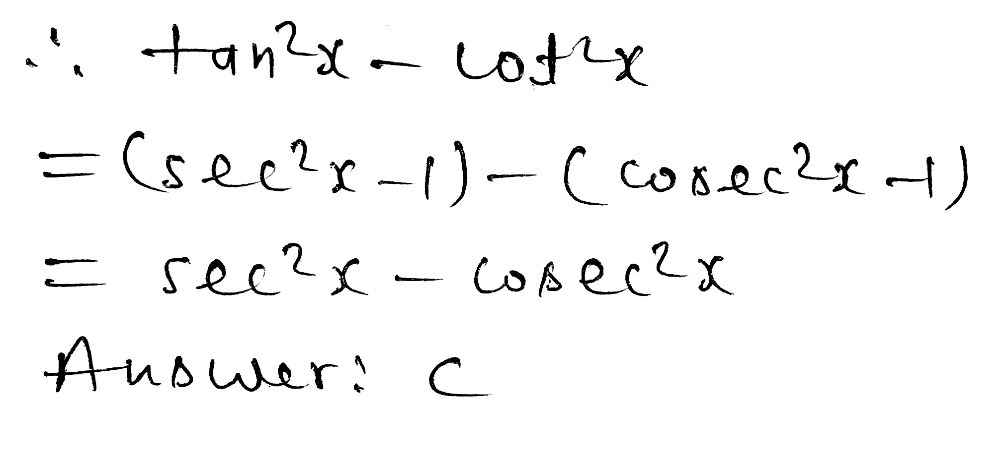
Use Trig Identities To Simplify Tan 2x Cot 2x A Gauthmath

 Find the values of the other five trigonometric functions Example 321 2 tan ⁡ θ = − 5 12, π 2 < θ < π Solution First, we know that \theta is in the second quadrant, making sine positive and cosine negative For this problem, we will use the Pythagorean Identity 1 tan 2 ⁡Trigonometry Trig identity $1\tan x \tan 2x = \sec 2x$ Mathematics Stack Exchange Trig identity 1 tan ⁡ Use the fundamental identities to simplify the expression cot beta sec beta I used 1tan^2u=secu since cot is the inverse of tan I flipped the tangent, then so it was 1 (1/tan) But the book's answer is the cosecant of beta

1

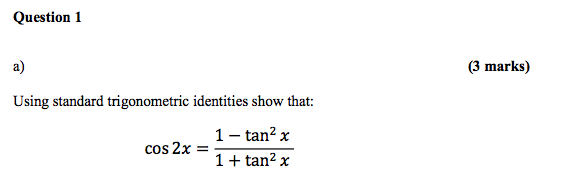
A Using Standard Trigonometric Identities Show That Chegg Com

We can prove the double angle identities using the sum formulas for sine and cosine From these formulas, we also have the following identities sin ⁡ 2 x = 1 2 ( 1 − cos ⁡ 2 x) cos ⁡ 2 x = 1 2 ( 1 cos ⁡ 2 x) sin ⁡ x cos ⁡ x = 1 2 ( sin ⁡ 2 x) tan ⁡ 2 x = 1 − cos ⁡ 2 x 1 cos ⁡ 2 x I was practicing some integration when I came across a problem that required the trig identity $\tan^2(x) = \sec^2(x)1$ However, I have never come across this identity and would like to know how it's derived trigonometry Share Cite Follow edited Nov 5 '18 at 918 BlueAs the length of the perpendicular and base is given;

Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com

Trigonometric Identities Trigonometric Functions Trigonometry

 please help me use trig identities to find the exact value tan 25° tan 5° / 1 tan 25° tan 5° math If sinθ=7/13 and cosθ=12/13 find tan θ and cot θ Use Pythagorean Identities to find sin θ and tan θ if cos θ =24/25 if the terminal side of θ lies in the third quadrantAnswer to Establish the identity (1 sin^2 x)(1 tan^2 x) = 1 By signing up, you'll get thousands of stepbystep solutions to your homeworkThe limits of those three quantities are 1, 1, and 1/2, so the resultant limit is 1/2 Proof of compositions of trig and inverse trig functions All these functions follow from the Pythagorean trigonometric identity We can prove for instance the function ⁡ ⁡ () =

Ch 7 Trigonometric Identities And Equations Ppt Video Online Download

How Do You Solve 1 Tan 2x 6 2sec 2x Socratic

Los uw wiskundeproblemen op met onze gratis wiskundehulp met stapsgewijze oplossingen Onze wiskundehulp ondersteunt eenvoudige wiskunde, prealgebra, algebra, trigonometrie, calculus enMath Cheat Sheet for Trigonometry This website uses cookies to ensure you get the best experienceAlgebra > Trigonometrybasics> SOLUTION Verify this identity (tan^2(x)1)/(1tan^2(x)) = 12cos^2(x) I've started a couple different options but none are working out for me

How To Prove Quotient And Reciprocal Identities Studypug

Using Trigonometric Identities Video Khan Academy

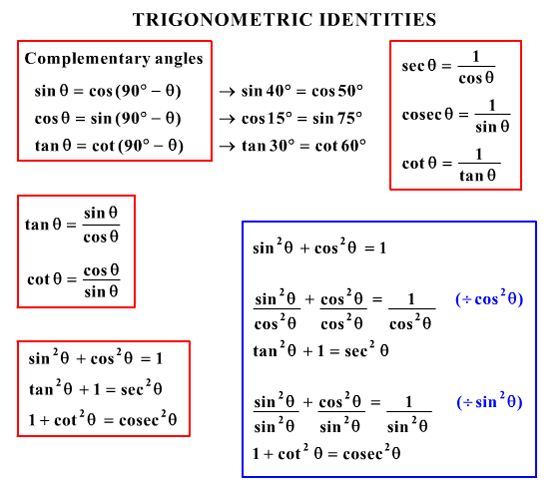
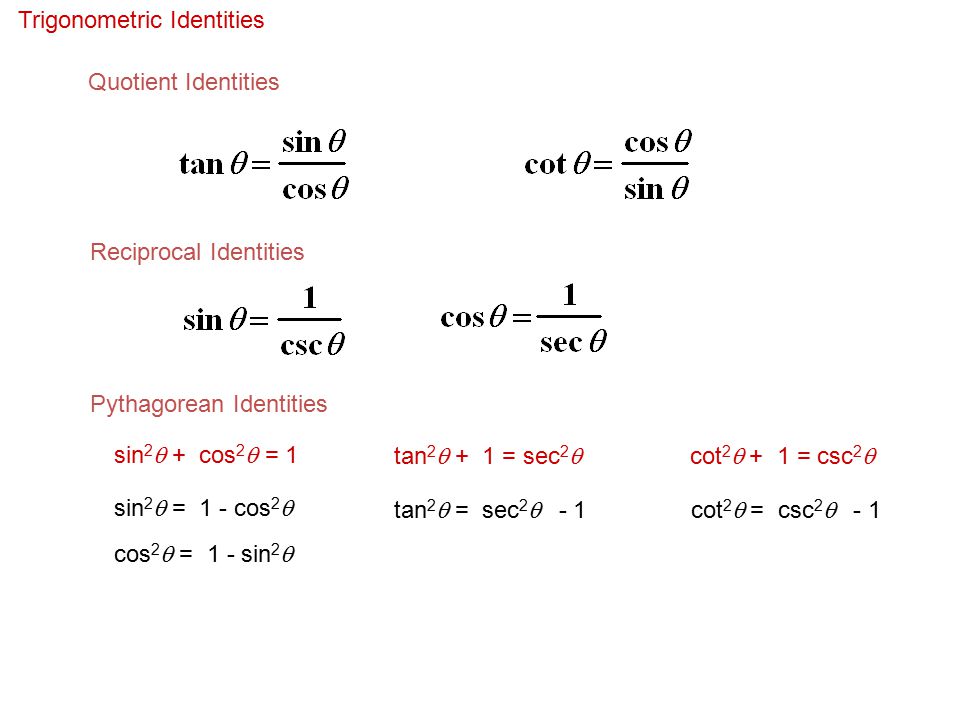
 Here we will prove the problems on trigonometric identities As you know that the identity consists of two sides in equation, named Left Hand Side (abbreviated as LHS) and Right Hand Side (abbreviated as RHS)To prove the identity, sometimes we need to apply more fundamental identities, eg $\sin^2 x \cos^2 x = 1$ and use logical steps in order to lead oneIdentities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4 cot x = 1/tan x equation 5 sin 2 x cos 2 x = 1 equation 6 tan 2 x 1 = sec 2 x equation 7 1 cot 2 x = csc 2 x equation 8 cos (x y) = cos x cos y sin x sin y equation 9 sin (x y) = sin x cos y cos x sin y equation 10 cos (x) = cos x equation 11Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!

What Would Be Steps In Proving That Tan2x Secx 1 1 Sec X Socratic

Cos2x Identity

(1/sin 2 x) 2 = (1/tan 2 x) 2y Identity used cosec 2 x cot 2 x = 1 Explanation (1/sin 2 x) 2 = (1/tan 2 x) 2y ⇒ cosec 2 x 2 = cot 2 x 2y ⇒ cosec 2 x cot 2 x 2 = 2y ⇒ 1 2 = 2y ∴ The value of y is 3/2Tan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos 2 (x) sin 2 (x) = 2 cos 2 (x) 1 = 1 2 sin 2 (x) tan(2x) = 2 tan(x) / (1Verify the identity 1 cos 2x tan x = sin 2x Use the appropriate doubleangle formulas to rewrite the numerator and dena simplified 1 cos 2x sin 2x 1 Simplify the numerator Enter denominator found in the previ The expression from the previous step then simplifies to tan x using what?

Web Stanford Edu Class Archive Math Math Math 1144 Files Trig Pdf

Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube

 1 tan 2 x = sec 2 x So, tan 2 x = sec 2 x 1 Thus, 1 tan 2 x = 1 (sec 2 x 1) = 2 sec 2 xIdentity\\sin^2(x)\cos^2(x) trigonometricidentitycalculator prove sec^{4}(x)=12tan^{2}(x)tan^{4}(x) en Related Symbolab blog posts I know what you did last summerTrigonometric Proofs To prove a trigonometric identity you have to show that one side of the equation can be transformed into the other

Trig Identities Hsn Forum

Using Standard Trigonometric Identities Show That Chegg Com

Establish The Identity 1 Sin 2 X 1 Tan 2 X 1 Youtube

Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x

Which Of The Following Expressions Completes The Identity 1 Sec 2 X Mathematics Stack Exchange

5 1 Fundamental Trig Identities Reciprocal Identities Sin

11 Basic Trigonometric Identities An Identity Is An Equation That Is True For All Defined Values Of A Variable We Are Going To Use The Identities To Ppt Download

Q Tbn And9gctg1mv4zqwzzx9es1vyuwisok4cikumrujuyo2nyqlvyw5qkqqv Usqp Cau

Reader011 Fdocuments In Reader011 Slide

Weierstrass Substitution Wikipedia

Biomath Trigonometric Functions

Tan2x ただの悪魔の画像

Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube

Integrate Sec 2x Method 2

Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube

Every Day I M Calculatin I D3 Unit Q Pythagorean Identities

Integrate Sec 2x Method 1

Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube

Analytic Trig Ppt Video Online Download

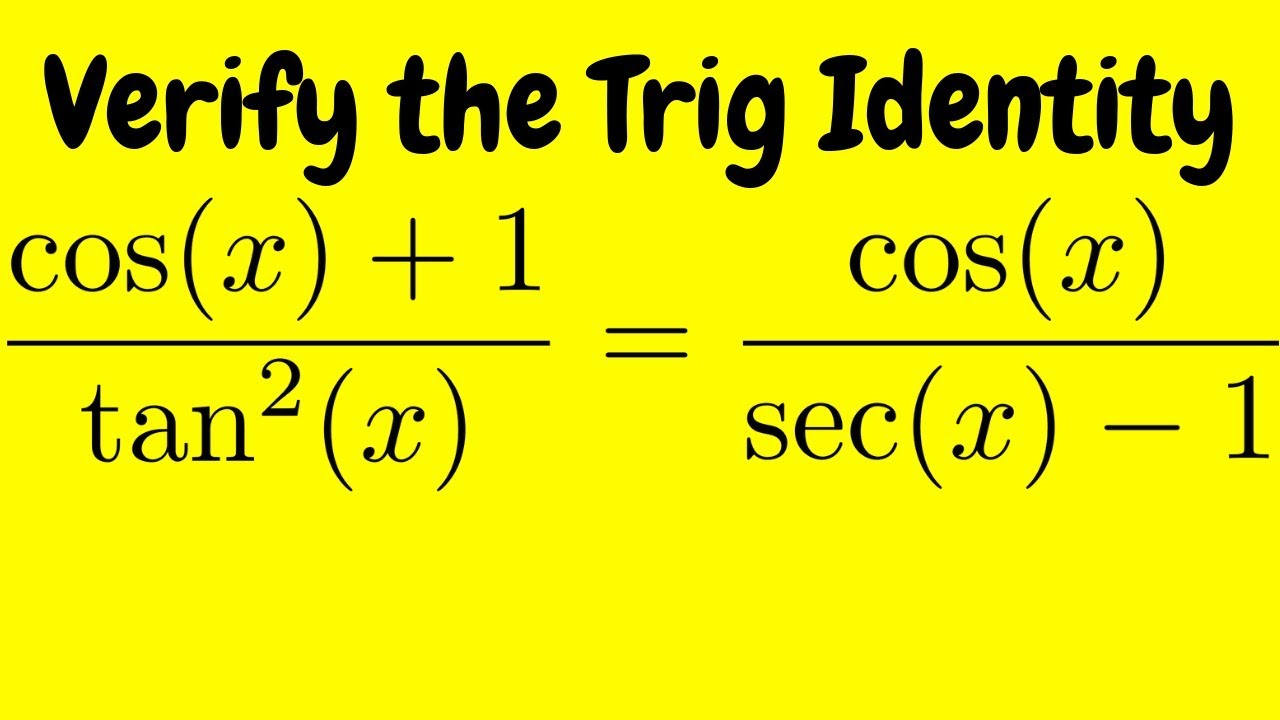
Verifying A Trigonometric Identity Cos X 1 Tan 2 X Cos X Sec X 1 Youtube

Magic Hexagon For Trig Identities

Cos2x Identity

Tan2x ただの悪魔の画像

Trig Double Identities Trigonometric Double Angle Functions Trig

Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero

2 Prove The Following Trig Identities A Prove Tan Chegg Com

Trigonometric Identities Edexcel A Level Maths Pure Revision Notes

What Is The Formula Of Tan2x Quora

Trig Identities Hsn Forum

10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com

Http Scibug Com Public Docs Trigonometry Cheat Sheet Pdf

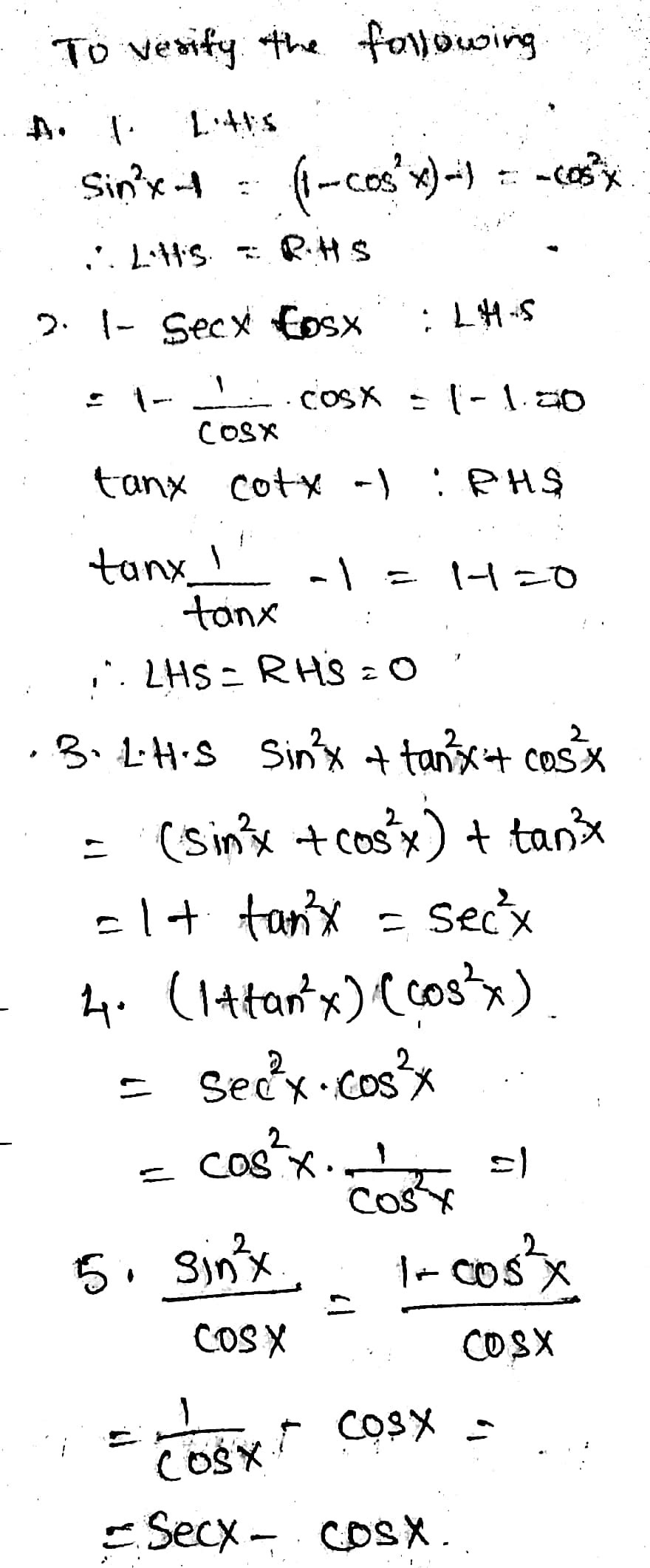
Directions Verify The Following Trigonometric Id Gauthmath

Www Alamo Edu Contentassets 35e1aad11a064ee2ae161ba2ae3b2559 Analytic Math2412 Double Angle Power Reducing Half Angle Identities Pdf

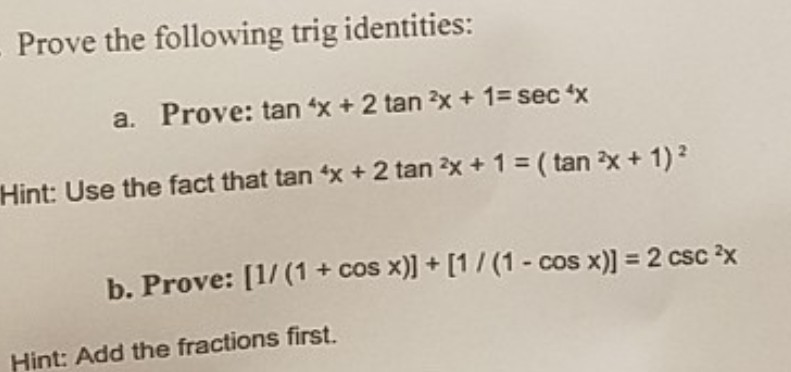
Prove The Following Trig Identities A Prove Tan X Chegg Com

A Trig Identity

1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube

2

Math34 Trigonometric Formulas

Www2 Math Binghamton Edu Lib Exe Fetch Php People Mckenzie Trig Identities Worksheet With Answers 2 Pdf

Tan 2x Csc 2x Tan 2x 1 Problem Solving Solving Identity

How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic

Integrate Sec 2x Method 2

Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download

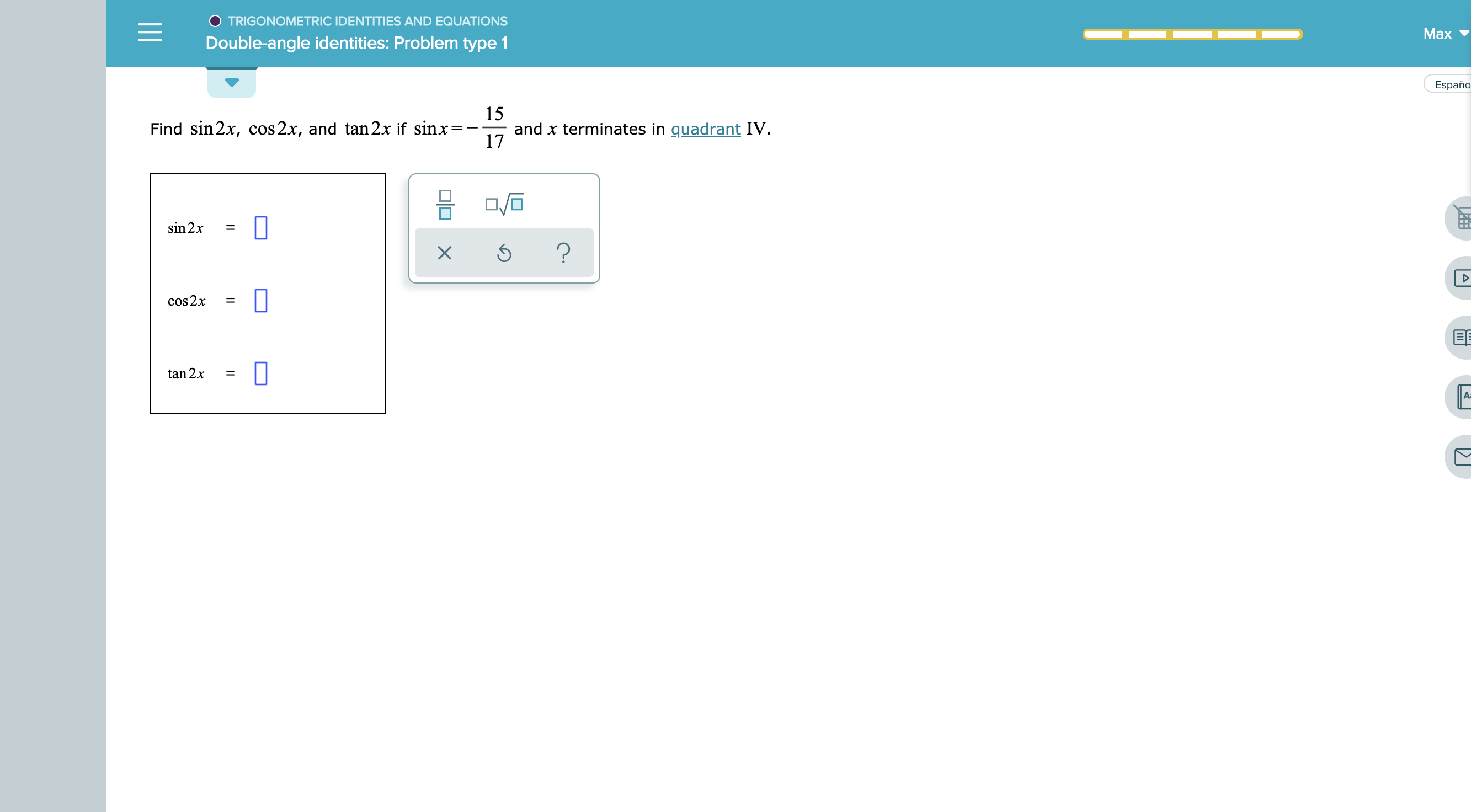
O Trigonometric Identities And Equations Double Angle Identities Problem Type 1 3 Find Sin 2x Cos 2x Homeworklib

Trigonometric Identities And Examples With Worksheets

How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic

Tan2x ただの悪魔の画像

How Do You Prove Tan 2x Secx 1 1 Secx Socratic

Jami Wang Period 3 Extra Credit Ppt Pythagorean Identities Sin 2 X Cos 2 X 1 Tan 2 X 1 Sec 2 X 1 Cot 2 X Csc 2 X These Identities Can Be

Derivatives Of Trigonometric Functions

Trig Identities The Student Room

5 1 Fundamental Trig Identities Reciprocal Identities Sin

Inverse Trig Identities Reciprocal Of Trigonometric Function Trig

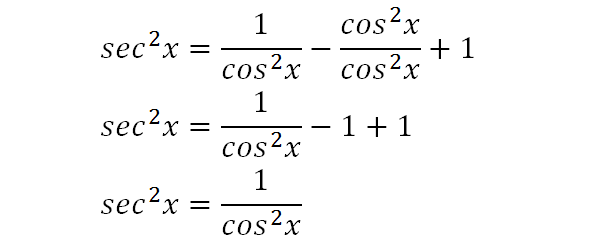
Integrate Sec 2x Method 2

Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco

3

Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions

Www Drfrostmaths Com Resources Getfile Php Fid 12

Directions Verify The Following Trigonometric Id Gauthmath

How To Prove That 1 Sin 2x 1 Cotx Cos 2x 1 Tanx Sinxcosx Using Trig Identities Quora

Tan 2x Formula What Is Tan 2x Formula Examples

Math34 Trigonometric Formulas

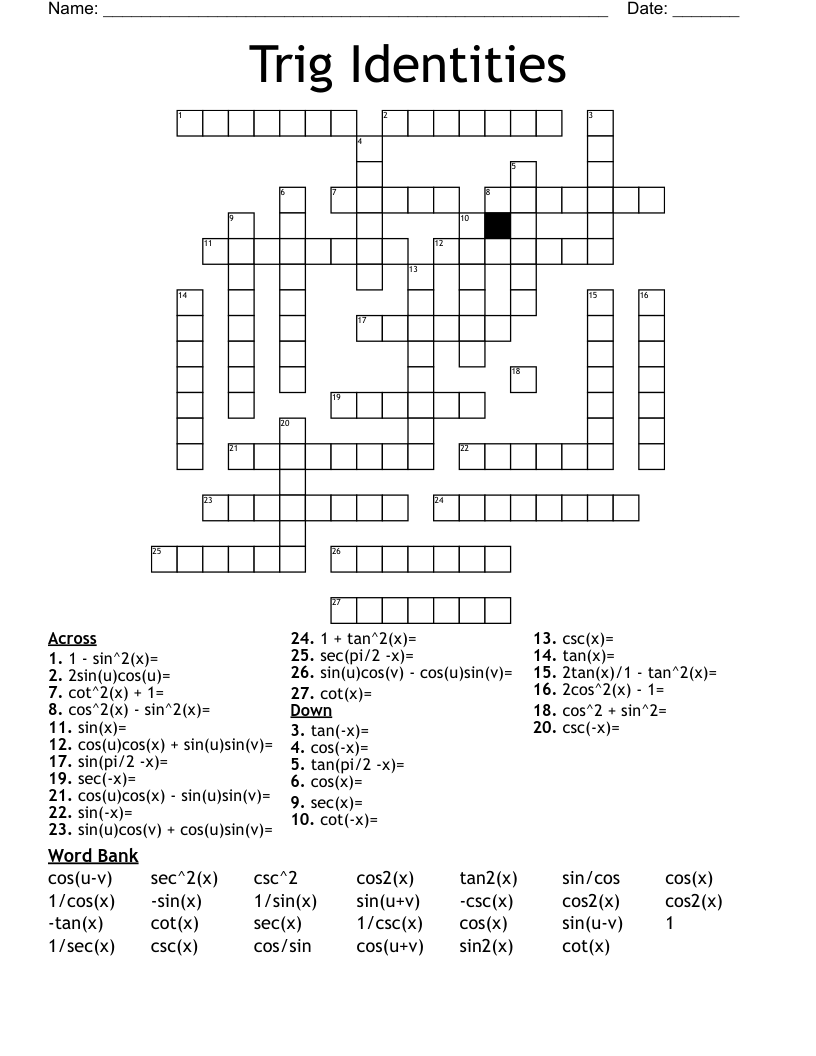
Trig Identities Crossword Wordmint

How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic

How To Use Trig Identities Mathematics Stack Exchange

Trig Identities Bingo Card

Prove Sin2x 2tanx 1 Tan 2x Socratic

Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download

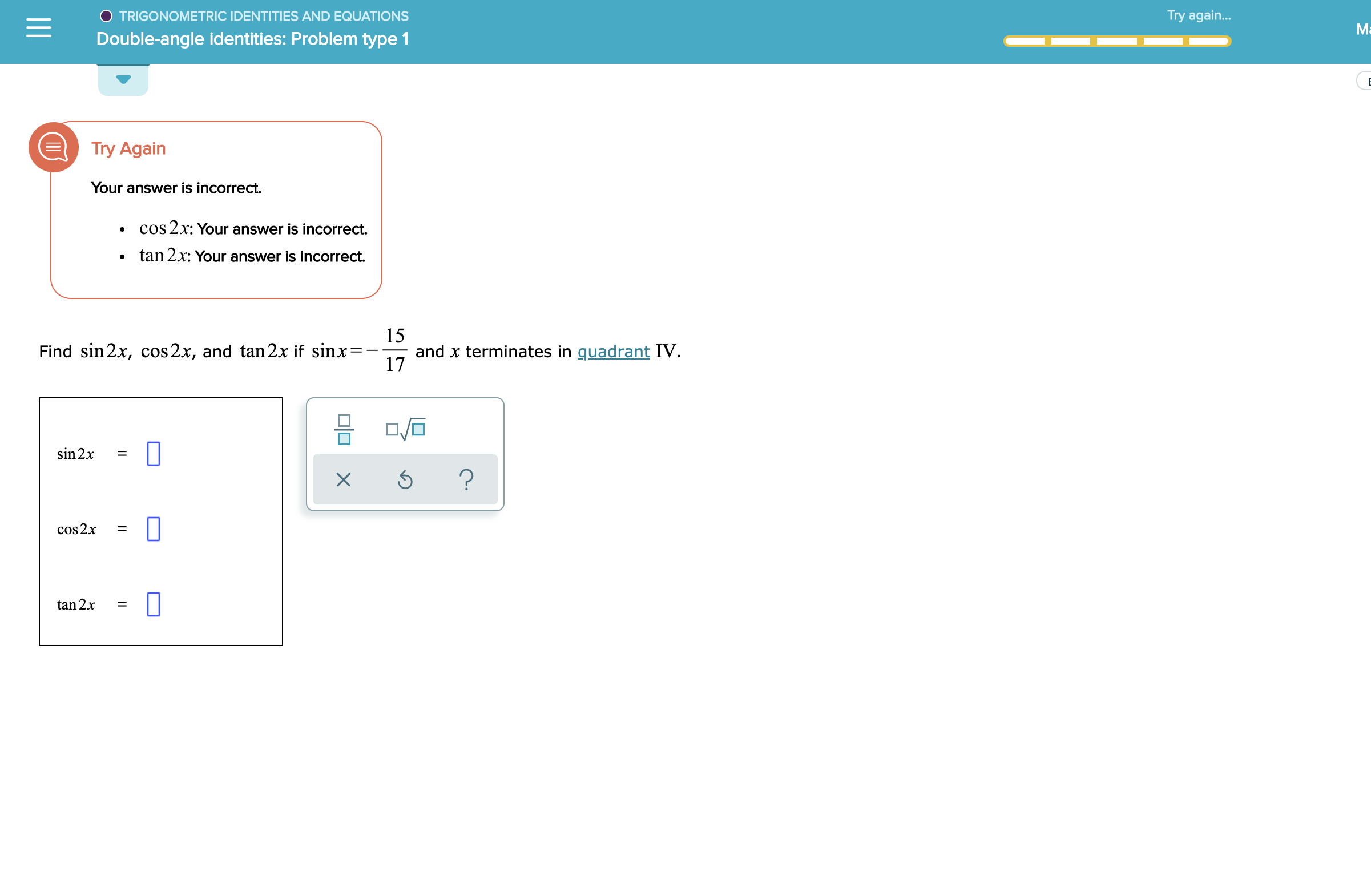
Answered O Trigonometric Identities And Bartleby

Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi

Qph Fs Quoracdn Net Main Qimg F1a1eec5e195

5 1 Fundamental Trig Identities Reciprocal Identities Sin

Math Problems Simplifying With Trigonometry Identities And Then Integration

7 4 Proving Trigonometric Identities Mhf4utrigonometry

1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube

Trigonometry Reciprocal Identities Expii

9 1 Identities And Proofs Ppt Download

What Is The Formula Of Tan2x Quora

Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions

1

Ilectureonline

Trig Identities Worksheet With Answers 2

Incoming Term: trig identities 1+tan^2x,